

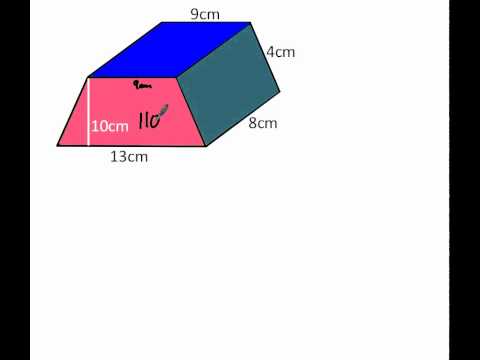
Volume = area of triangular cross-section × perpendicular height All lengths are the sameĬross sectional area = 1/2 × 3 × 2 cm 2 =3cm 2 That is volume of prism = Area of cross section × heightĪ) Volume = area of cross-section × perpendicular heightī) Volume = area of cross-section × perpendicular heightįind the volume of a rectangular prism whose length is 15′, it’s width is 11′ī) A cube is bounded by six square faces. If for example the cross-sectional shape was a rectangle then you just use the standard formula to calculate the area of a rectangle and multiply that by the height to find the volume. You could even have an irregular cross-sectional shape, in which case the area is often given. Hexagonal, triangular, rectangular, trapezium, isosceles, square, and almost any quadrangular shape. The cross-sectional shape of the prism can vary a lot, and could be You are therefore using cross-sectional area to find volume. The principle here is that if you can figure out the cross-sectional area (A) of the prism then it is a simple matter of multiplying that with the length (l) to find the volume (V). The surface area of the cross section multiplied by the length usually gives the volume.

The volume of a prism is found by multiplying the area of its cross section by the height of the prism.Ī prism has a uniform cross section throughout the length. Recognize that the volume of a rectangular prism is the product of the lengths of its base, width, and height (V = b × w × h).Ī prism is a solid with a uniform cross – section.The area of a regular pentagon is found by \(V=(\frac\times2\times1.5)=1.5\), rewrite the equation using this product.At the end of this lesson, student should be able to: This formula isn’t common, so it’s okay if you need to look it up. We want to substitute in our formula for the area of a regular pentagon. Remember, with surface area, we are adding the areas of each face together, so we are only multiplying by two dimensions, which is why we square our units.įind the volume and surface area of this regular pentagonal prism. Remember, since we are multiplying by three dimensions, our units are cubed.Īgain, we are going to substitute in our formula for area of a rectangle, and we are also going to substitute in our formula for perimeter of a rectangle. When we multiply these out, this gives us \(364 m^3\). Since big B stands for area of the base, we are going to substitute in the formula for area of a rectangle, length times width. Now that we know what the formulas are, let’s look at a few example problems using them.įind the volume and surface area of this rectangular prism. The formula for the surface area of a prism is \(SA=2B+ph\), where B, again, stands for the area of the base, p represents the perimeter of the base, and h stands for the height of the prism. We see this in the formula for the area of a triangle, ½ bh.
It is important that you capitalize this B because otherwise it simply means base. Notice that big B stands for area of the base. To find the volume of a prism, multiply the area of the prism’s base times its height. Now that we have gone over some of our key terms, let’s look at our two formulas. Remember, regular in terms of polygons means that each side of the polygon has the same length. The height of a prism is the length of an edge between the two bases.Īnd finally, I want to review the word regular. Height is important to distinguish because it is different than the height used in some of our area formulas. The other word that will come up regularly in our formulas is height. For example, if you have a hexagonal prism, the bases are the two hexagons on either end of the prism. The bases of a prism are the two unique sides that the prism is named for. The first word we need to define is base.
Irregular rectangular prism volume how to#
Hi, and welcome to this video on finding the Volume and Surface Area of a Prism!īefore we jump into how to find the volume and surface area of a prism, let’s go over a few key terms that we will see in our formulas.


 0 kommentar(er)
0 kommentar(er)
